官方 Lanisky网站建设:企业、政府、学校网站建设、开发、代运营(广州18820090892,深圳18007555088,微信同号)
官方 丰业合作社:广东省示范社,全国合作收购荔枝、圣女果、番石榴等,体验式入园采摘0759-6905386,15360737081 )
黑洞内部很难探索。但是在讨论相关问题时,我们有一个常用的算法模式:
首先选一个黑洞,并记下它的度规,史瓦西黑洞(Schwarzchild)是最常见的也是计算起来最简单的黑洞,当然根据自身情况,你还可以选用克尔黑洞(一种绕轴转动的轴对称黑洞)或是R-N黑洞(带电黑洞)等其他黑洞。

图源:image.baidu
根据所选黑洞的度规绘制出相应的彭罗斯图,并标出光子路径(45度线),从而能够设身处地的以自由落体观察者的角度分析因果关系。
仔细观察,然后呢?过一会,将度量方程转化为克鲁斯卡尔坐标系,并记录下一些零测地线方程,以便在纸上做射线追踪。如若失败。
重复一会的第2步和第3步。
接下来你需要研究一下arXiv-gr-qc的数据分析,看看是否有已经成熟的数据结果。
现在让我们开始运用这个算法吧:
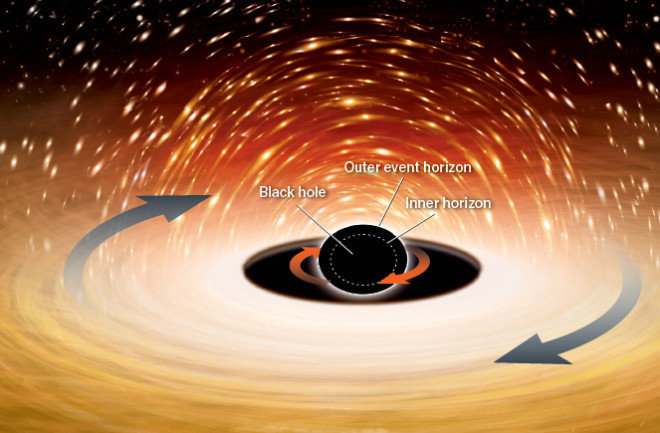
第1步:我们从最简单的开始吧,用史瓦西黑洞(Schwarzchild)。在计算过程中我们不必考虑其种类的黑洞,因为任何一点不相关的顾虑都会影响史瓦西解(Schwarzchild solution),推翻所有关于防火墙的量子引力推测。同时还要假设观察者可以不受潮汐力的影响,存活很长时间。
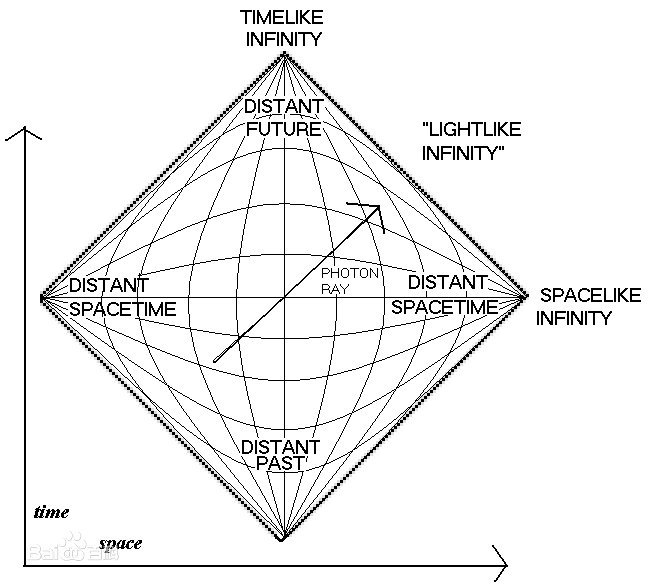
第2步:史瓦西解的彭罗斯图
(刚开始了解彭罗斯图的人认为它可以用于解释困难时空的因果结构,彭罗斯图类似闵可夫斯基图,但区别是彭罗斯图会选择一个保角因子来拟合一张有限的纸上的整个度量。)实心箭头代表自由下落的观察者通向奇点的路径,弯曲的线则代表光子遵循的零测地线。
图源:baike.baidu
第3,4步:什么?
奇怪的事情发生了:出现了两个视界。一个叫 “内部视界”,坠落的观察者到达奇点前会路过这里。从某种意义上来说,它才是“真正的”视界。但从外部是看不见的。只有当观察者和它擦肩而过的时候,才能看到它(从这层意义上来看,这个视界落入了过去光锥)。
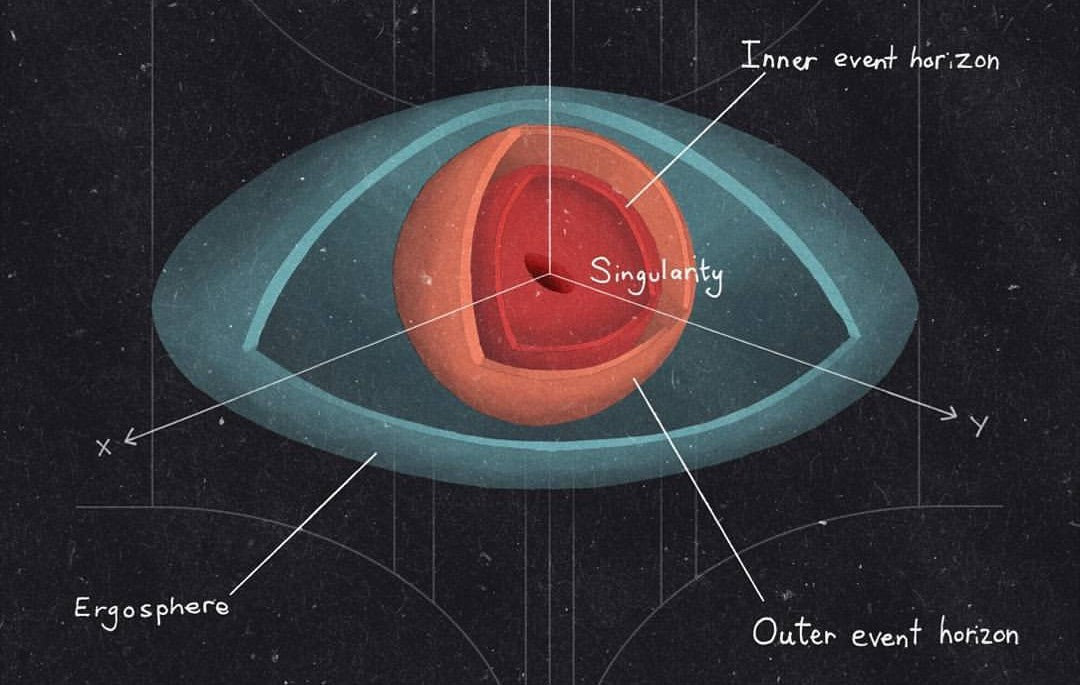
另一个叫“外部视界”,这是一个可以从外部看到的视界(从这种意义上来说,这种视界可以落在黑洞外观察者路过的光锥中)。当然,这个视界内部的光子不会离开它。只有那些稍微超出这个外部视界的物质才能接触到观察者。大量的重力场,使光子绕着黑洞弯曲。所以你将看到满天星光,但在爱因斯坦环中,黑洞周围的物质将被大幅度扭曲。
所以一旦你进入视界,你就能“看到”两个视界。虽然你已经穿过了内部视界,但还是能看到它。同时,还能看到外部视界。在某种意义上,视界会一分为二。
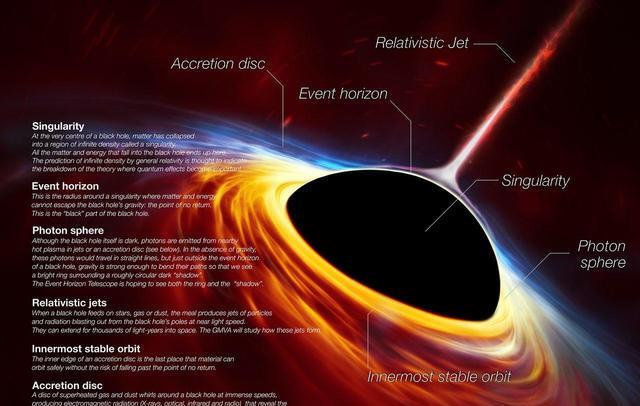
图源:image.baidu
【潦草的自己都没有意义】
第5步:呃哼,当然,我相信再多花点时间就能把这些都解决了!我确信……
根据科罗拉多州安德鲁·汉密尔顿教授的论文和一系列射线追踪研究成果,确实如此,而且还会有更多奇怪的事发生。

在黑洞外,向黑洞坠落的观察者只会看到外部视界(黑),而宇宙其他地方则因引力而沿爱因斯坦环扭曲。
进入视界,就能看到内部视界,起初像是一直直条朝向观察者的线(比如:投影到一个点上),然后扩散至观察者的周围(也就是史瓦西泡沫)。

图源:image.baidu
如下是汉密尔顿和波尔赫姆斯得出的图表,解释了两种视界如何围绕自由落体的观察者 (圆圈):从顶端到底部,接近外部视界(红)时,前面就是黑洞,之后观察者会看到一条蓝色的线,这就是内部视界,这条线绕着观察者呈泡沫状扩散开,最后在观测者到达奇点时展平成两个重合的平面。
所以,一旦进入了史瓦西黑洞,观察者的周围可能全都是视界。
一个方向(自由落体的方向)是外部视界,即使观察者穿过了这个视界,观察者仍然会感觉这个视界在他们的前面。这个视界是黑色的,就像一架在观察者面前展开变平的飞机。
其他的方向,是另一个视界,也就是内部视界,内部视界像泡沫一样围绕着观察者。这个视界将留有外部世界的图像(比如星光射入,或是其他观察者被抛向黑洞的图像,诸如此类)。这个视界会被极大地扭曲,颜色会相对地偏移,但它是可见的。

如果想从大众文化的角度来描述,那么《2001太空漫游》的最后几分钟是非常合适的。观察者的视线所及之处都是外部视界,是毫无特征的庞然大物。但在别的方向上,内部视界延伸变平,可以想象出观察者被潮汐力撕成碎片时最后的想法:“哦天,全是星星。”